Halflingen (Halflings) (1ste editie)
WikiCarpedia auteurs' disclaimer
De ontwerpers van Halflingen namen een grote gok door de tegelvorm aan te passen, die volledig afwijkt van het basisspel. We zijn nog lang niet zeker of dit experiment een succes was, maar we voelen ons verplicht om een paar uitspraken te doen.
Door heel WikiCarpedia volgen wij de feiten en de officiële verduidelijkingen maar in het geval van Halflingen is dat bijna onmogelijk aangezien deze niet door de uitgever, HiG, wordt ondersteund. Door zijn unieke karakter is het zelfs moeilijk om een allesomvattende set spelregels uit te werken die antwoord geven op alle openstaande kwesties die zich kunnen voordoen bij de interactie met andere uitbreidingen.
Hoe het ook zij, wees gewaarschuwd dat je bij het spelen met de Halflingen situaties tegen kunt komen die hier niet beschreven worden. Niet omdat we niet bekend waren met deze situaties, maar omdat we geen antwoorden hebben kunnen vinden in de officiële verhelderingen. Voel je in zulke gevallen vrij om je eigen huisregels te bedenken en lol te hebben!
Algemene informatie en opmerkingen
Halflingen is oorspronkelijk uitgebracht in Spielbox en in 2014 uitgegeven door Hans im Glück.
De mini-uitbreiding Halflingen (of “Half & Half”) was in twee versies verkrijgbaar. Één versie is verkrijgbaar in de 5/2014 uitgave van Spielbox-magazine (www.spielboxshop.de) en deze tegels zijn gemarkeerd met een vijfhoek. De tweede versie was verkrijgbaar in de webshop van Hans im Glück (www.cundco.de) en deze tegels zijn gemarkeerd met een “C”-Horige. Het is daardoor mogelijk dat er in onderstaande voorbeelden tegels voorkomen die geen deel uitmaken van de “Halflingen” die jij hebt.
Een latere heruitgave van deze uitbreiding werd vergezeld van een grote revisie van de verhelderingen die op deze pagina staan. In de meest recente spelregels heeft bij verschillende interacties het raster van tegels voorrang op individuele tegels. De meest recente spelregels vind je hier.
Speelmateriaal
- 12 nieuwe “halve” driehoekige landtegels (Spielbox: Halflingen I)
- 12 nieuwe “halve” driehoekige landtegels (Cundco: Halflingen II)
Spelregels
Voorbereiding
Deze mini-uitbreiding kan met maximaal 6 spelers gespeeld worden. Met extra exemplaren, kun je met meer dan 6 spelen. Voor het eerste spel met deze mini-uitbreiding raden we aan om alle driehoekige tegels gedekt door elkaar te husselen en er elke speler twee te geven. De spelers bekijken hun tegels en leggen die weer gedekt voor zich neer op tafel. Als de spelers meer bekend zijn met de nieuwe tegels, kunnen ze de volgende variant proberen: aan het begin van het spel worden alle driehoekige tegels open op tafel gelegd. Er wordt een startspeler bepaald. Te beginnen met de speler die als laatste aan de beurt zou zijn, en dan tegen de klok in, neemt iedereen één tegel en legt die gedekt voor zich neer. Op dezelfde manier nemen alle spelers een tweede tegel. Op die manier heeft elke speler 2 tegels gekozen om tijdens het spel te gebruiken. [1] [2] [3]
Met uitzondering van de nieuwe regels die bij deze mini-uitbreiding worden gebruikt, blijven alle basisregels van Carcassonne ongewijzigd.
Landtegel leggen
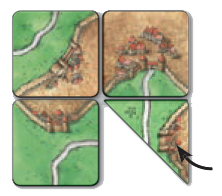
Als een speler aan de beurt is, mag hij een van zijn twee driehoekige tegels spelen in plaats van een normale tegel te nemen. De driehoekige tegels worden volgens de gebruikelijke regels geplaatst; ze moeten zo geplaatst worden dat minstens één van de korte zijden van de tegel een eerder geplaatste tegel raakt (niet alleen hoek-tot-hoek) of de langere zijde de langere zijde van een andere driehoekige tegel raakt.
Bovendien moeten alle stads-, weg- en veldsegmenten die al in het spel zijn, doorgaan met segmenten die al in het spel zijn. De langere zijde van een driehoekige tegel mag nooit tegen de zijde van een normale tegel worden geplaatst.
Tegels met projecten van uitbreidingen: Sommige tegels van de versie van CundCo bevatten projecten uit de uitbreidingen Schapen en Heuvels en De Graancirkels [4] [5]. Als je Halflingen niet met die uitbreidingen speelt, kun je die projecten negeren.
Heuvels: Als een speler een driehoekige tegel aanlegt met een heuvel en je speelt met de uitbreiding Schapen en Heuvels, dan trekt de speler onmiddellijk een tweede (normale) tegel, volgens de spelregels van Schapen en Heuvels, en legt die gedekt onder de driehoekige tegel. De andere “helft” van de gedekte tegel mag later met een andere driehoekige tegel bedekt worden. Beide driehoekige tegels worden tot dezelfde heuvel gerekend.
Puntentelling
BELANGRIJKE OPMERKINGEN
- Opmerking 1 - Gewijzigde spelregels: Na de oorspronkelijke spelregels van 2014, werd de puntentelling van deze uitbreiding in 10/2015 gewijzigd.
- Oorspronkelijke spelregels: een driehoekige tegel wordt op dezelfde manier geteld als een normale landtegel. Als er 2 driehoekige tegels in hetzelfde vierkante “vak” liggen, tellen ze voor de puntentelling van een project (weg, stad of klooster) nog steeds voor 1 (gecombineerde) tegel.
- Nieuwe spelregels: een driehoekige tegel wordt op dezelfde manier gesteld als een normale landtegel. Als er twee driehoekige tegels in hetzelfde vierkante “vak” liggen, tellen ze elk voor 1 punt bij het tellen van een project (weg, stad of klooster).
- Onderstaande spelregels voor de puntentelling gaan uit van de nieuwe regels.
- Opmerking 2 - Onduidelijke basisregels: Als gevolg van het gebrek aan duidelijkheid in de oorspronkelijk spelregels en de latere, tot op heden verschafte, verhelderingen, zijn driehoekige gaten een bron van controverse met betrekking tot:
- Afgebouwde projecten: Het is onduidelijk of een project met driehoekige gaten als afgebouwd moet worden beschouwd en dus geteld kan worden. De oorspronkelijke puntentellingsregels (en latere verhelderingen) houden alleen rekening met kloosters, maar zeggen niets over steden, wegen of weiden waarover talloze vragen bestaan zonder formeel antwoord. [6] [7]
- Onbepaalde interactie met andere uitbreidingen: De onderbrekingen in het landschap als gevolg van driehoekige gaten hebben gevolgen voor de spelmechanismen en/of puntentelling van verschillende andere uitbreidingen. Als die er al zijn, zijn er slechts gedeeltelijke verhelderingen bekend over hoe met de ontdekte gevallen omgegaan moet worden.
- HiG zal geen verdere verhelderingen meer leveren. Op grond van de bestaande spelregels en de snippers aan verhelderingen, proberen spelers wat huisregels te extrapoleren om de kwesties waar ze tegenaan lopen op te lossen, maar er kan geen consensus worden bereikt.
Puntentellingen afhandelen [8]
Kloosters: Als er met Halflingen wordt gespeeld, wordt een klooster als afgebouwd beschouwd, ook als op één of meer van de omliggende vakken een driehoekige tegel ligt. In dat geval telt een driehoekige tegel als een normale landtegel (1 punt per tegel die het klooster omringt.) Als er 2 driehoekige tegels op hetzelfde vierkante “vak” liggen, telt elk daarvan voor 1 punt voor het tellen van het klooster. [9] [10]
Eindtelling
Het spel eindigt onmiddellijk aan het einde van de beurt waarin de laatste normale landtegel is aangelegd. Als er nog spelers zijn die ongebruikte driehoekige tegels voor zich hebben liggen, mogen ze die niet meer aanleggen. Nu vindt de eindtelling plaats. [11]
Andere uitbreidingen
>> Algemene overwegingen
- Als een Halfling-tegel naast een driehoekig gat ligt, telt de Halfling-tegel als een afzonderlijke tegel. Als er twee Halfling-tegels samen een vierkant vormen, tellen ze elk als een afzonderlijke tegel. Dit is van belang bij het tellen van kloosters, steden, wegen, bescherming door de fee, de jacht van de draak, het leggen van pest-fiches, vliegen met de vliegtuigen, enz. (10/2014; bijgewerkt 10/2015)
- HiG geeft momenteel geen ondersteuning op de uitbreiding Halflingen en zal geen verdere verhelderingen meer verschaffen. Halflingen combineren met andere uitbreidingen is dus "op eigen risico van de spelers". In dergelijke gevallen zullen er dus huisregels moeten worden afgesproken die kunnen worden toegepast.
>> De Draak, de Fee en de Jonkvrouw - Bescherming door de fee
- Er is, buiten bovenstaande algemene overwegingen, geen officiële verheldering over hoe de fee zich gedraagt als ze op een Halfling-tegel staat. Derhalve kunnen we aannemen dat de fee alleen de driehoekige tegel beschermt waar ze op staat, aangezien het een afzonderlijke tegel is.
>> De Draak, de Fee en de Jonkvrouw (1e editie) - De draak gaat op jacht!
- Er is geen officiële verheldering over hoe de draak zich over Halfling-tegels verplaatst, ander dan de algemene overwegingen hierboven.
- Opmerkingen:
- Spelregelverheldering: Bij de jacht van de draak worden de driehoekige tegels als aparte tegels beschouwd.
- Openstaande vraag: Mag aangenomen worden dat de draak een driehoekig gat mag passeren? Verhelderingen voor andere uitbreidingen zoals De Pest (zie onder), geven aanleiding tot een positief besluit, maar er is geen officiële bevestiging.
>> De Toren - Torenbereik
- Er is, buiten de algemene overwegingen hierboven, geen officiële verheldering beschikbaar hoe het bereik van de toren berekend moet worden als er Halflingen in het spel zijn.
- Opmerkingen:
- Spelregelverheldering: Bij het berekenen van het aantal tegels dat binnen het bereik van de toren valt, worden driehoekige tegels als afzonderlijke tegels beschouwd.
- Openstaande vraag: Mag aangenomen worden dat driehoekige gaten, indien aanwezig, genegeerd worden bij het berekenen van het bereik van de toren? Verhelderingen voor andere uitbreidingen zoals Duitse/Nederlandse en Belgische kloosters (zie onder), geven aanleiding tot een positief besluit, maar er is geen officiële bevestiging.
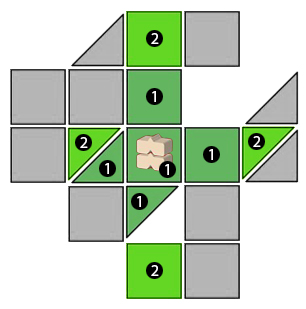 Voorbeeld: De afbeelding laat door verschillende kleuren groen voor bereik 1 en bereik 2 zien welke tegels geraakt worden door de toren. Voor de lengte van het bereik tellen driehoekige tegels afzonderlijk mee en worden driehoekige gaten overgeslagen. Het overslaan van driehoekige gaten is niet expliciet officieel bevestigd.
Voorbeeld: De afbeelding laat door verschillende kleuren groen voor bereik 1 en bereik 2 zien welke tegels geraakt worden door de toren. Voor de lengte van het bereik tellen driehoekige tegels afzonderlijk mee en worden driehoekige gaten overgeslagen. Het overslaan van driehoekige gaten is niet expliciet officieel bevestigd.
>> Burgemeesters en abdijen - Deel 1: Abdij leggen en tellen
- Een abdij mag gelegd worden als er aan één van de zijden een Halfling-tegel ligt, zelfs als er een driehoekig gat aan een van de zijden is. Zie de verhelderende afbeeldingen hieronder. (3/2015)
- Er is behalve de beslissing over kloosters, geen expliciete officiële bevestiging over hoe de puntentelling van abdijen werkt in combinatie met de Halflingen.
- Opmerkingen:
- Huisregel: De puntentelling voor een abdij volgt de officiële spelregels die voor kloosters zijn vastgelegd.
>> Burgemeesters en Abdijen - Deel 2: Herenboerderij zetten
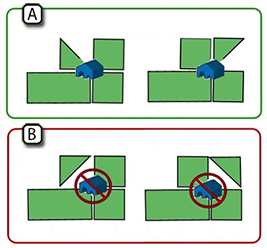
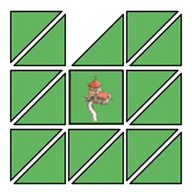
- Een herenboerderij mag gezet worden waar op alle 4 de hoeken van de kruising tenminste één tegel ligt, zelfs als daar halve tegels bij betrokken zijn. (10/2015)
- Verder zijn de spelregels voor het zetten van de herenboerderij als volgt bijgewerkt: De ondergrond voor de herenboerderij moet stabiel zijn zodat hij niet wiebelt. Dit betekent dat onder de herenboerderij:
- alle tegels elkaar in het midden moeten raken;
- geen van de kwadranten in het midden leeg mag zijn; en
- alle tegels in het in het midden een weide tonen om de herenboerderij op te zetten.
- Zie onderstaande voorbeelden met Halfling-tegels en dubbele tegels (zie Duitse Burchten.) (04/2016)
- Opmerking: De bijgewerkte spelregels van 10/2015 schuiven in sommige gevallen het oorspronkelijke vereiste van een kruispunt van vier tegels om een herenboerderij te mogen zetten zoals oorspronkelijk gedefinieerd voor vierkante tegels terzijde. Dit gebeurt ten faveure van een stabiele ondergrond voor de herenboerderij als er tegels met andere vormen in het spel zijn, zoals te zien in de voorbeelden met dubbele en/of driehoekige tegels.
>> Burgemeesters en Abdijen - Deel 3: Puntentelling van de herenboerderij
- Er zijn geen officiële spelregels die bepalen hoe de herenboerderij zich verhoudt tot onderbrekingen in het landschap die veroorzaakt kunnen worden door Halflings.
- Opmerkingen:
- Openstaande vraag: Mogen driehoekige gaten als gaten in de weide gezien worden? Zo ja, dan kunnen bepaalde tegelconfiguraties ertoe leiden dat er aparte weiden ontstaan die bij een kruispunt samenkomen, waarvan sommigen in aanmerking kunnen komen voor het zetten van een herenboerderij. Er is geen officiële spelregel of verheldering die zegt welke invloed driehoekige gaten hebben op weiden.
- Openstaande vraag: Als de herenboerderij op een kruispunt wordt gezet waar verschillende weiden samenkomen, worden die dan daardoor verbonden tot één grote weide? Er is geen officiële spelregel of verheldering op dit punt, maar de officiële spelregels voor het zetten van een herenboerderij zijn ervoor ontworpen dat die altijd op één enkele weide wordt gezet.
- Huisregel 1: Driehoekige gaten worden (net als vierkante) als grenzen van het landschap gezien en dus kunnen verschillende weiden bij een kruispunt samenkomen en toch gescheiden zijn.
- Huisregel 2: Om de herenboerderij (geldig) te mogen zetten op een punt waar meerdere weiden samenkomen, moeten ze als één enkele weide worden beschouwd. Dit lijkt redelijk omdat het leggen van aanvullende Halfling-tegels om de gaten te vullen de voorgaande situatie niet zou wijzigen maar slechts het aangenomen doorlopen van het landschap verwerkelijkt. Bovendien zijn dan alle spelregels voor de puntentelling van herenboerderijen van toepassing zoals gebruikelijk.
>> Ketters en Cultusplaatsen - Puntentelling van cultusplaatsen
- Er is behalve de beslissing over kloosters, geen expliciete officiële bevestiging over hoe de puntentelling van cultusplaatsen werkt in combinatie met de Halflingen.
- Opmerking:
- Huisregel: De puntentelling van een cultusplaats volgt de officiële spelregels die voor kloosters gelden.
>> Bruggen, Burchten en Bazaars - Bruggen bouwen
- Er is geen officiële verheldering met betrekking tot het gebruik van bruggen in combinatie met de Halflingen.
- Opmerkingen:
- Openstaande vraag: Mag een brug op een vak gezet worden waar maar één Halfling ligt?
- Huisregel: Een huisregel zou in navolging van de verhelderingen voor de herenboerderij uit Burgemeesters en Abdijen (zie boven) het bouwen van een brug alleen kunnen toestaan als de brug op een stabiele ondergrond staat. Dat zou betekenen dat een brug gebouwd kan worden als er een vierkante tegel of twee Halflingen in het betreffende vak liggen, maar niet als er maar één Halfling ligt.
>> De Vliegtuigen – Vliegafstand en landing
- Er is buiten de algemene overwegingen hierboven geen officiële verheldering hoe je om moet gaan met de vliegafstand en het landen als er Halflingen bij betrokken zijn.
- Opmerkingen:
- Verheldering van de spelregels: Bij het bepalen van de vliegafstand tellen driehoekige tegels als aparte tegels.
- Openstaande vraag: Mag je dan aannemen dat driehoekige gaten, als die er zijn, genegeerd moeten worden en alleen de halve tegels meegeteld worden voor het bepalen van de vliegafstand? Verhelderingen voor andere uitbreidingen zoals Duitse Kloosters / Kloosters in Nederland en België (zie onder), lijken dit te bevestigen, maar er is geen officiële bevestiging. Zie onderstaande voorbeelden die deze aanname volgen.

- Openstaande vraag: Wat doe je als het vliegtuig dat diagonaal vliegt, moet landen op een vak waar twee driehoekige tegels liggen waarvan de lange zijde in het verlengde ligt van de vliegrichting? Hiervoor bestaat geen officiële verheldering. Je huisregel kan vastleggen dat de speler dan zelf een project op één van beide tegels mag kiezen.
 Voorbeeld 5: Op deze afbeelding is te zien hoe om moet worden gegaan met driehoekige tegels bij het bepalen van de vliegafstand voor een diagonale vlucht. Dankzij de ligging van de Halflingen zijn er in dit bijzondere geval twee tegels met afstand 1. Met een huisregel kun je afspreken dat het vliegtuig bij die afstand dan op door de speler te kiezen tegel landt.
Voorbeeld 5: Op deze afbeelding is te zien hoe om moet worden gegaan met driehoekige tegels bij het bepalen van de vliegafstand voor een diagonale vlucht. Dankzij de ligging van de Halflingen zijn er in dit bijzondere geval twee tegels met afstand 1. Met een huisregel kun je afspreken dat het vliegtuig bij die afstand dan op door de speler te kiezen tegel landt.
- Huisregel: Je kunt een huisregel afspreken dat vierkante tegels, vierkante gaten en driehoekige tegels meetellen voor het bepalen van de vliegafstand. Als de landingszone twee driehoekige tegels bevat die dezelfde afstand hebben, mag de speler zelf kiezen.
>> De Pest – Verspreiding van de pest
- Een enkel driehoekig gat voorkomt niet dat de Pest zich in die richting verspreidt. (10/2015)
>> Duitse Kloosters/Kloosters in Nederland en België - Punten tellen voor de abt
- Een driehoekige tegel neemt de plaats in van een gewone landtegel. Een los driehoekig gat in het landschap is dus geen onderbreking van de rij of kolom voor het tellen van een abt op een Duits, Nederlands of Belgisch Klooster. Alleen als het een gat ter grootte van een normale landtegel is, wordt de rij of kolom onderbroken. (3/2015)
- Op de volgende afbeelding is te zien dat driehoekige tegels afzonderlijk geteld worden bij het tellen van een abt op een Duits klooster. Je ziet hier ook dat driehoekige gaten genegeerd worden.
 Voorbeeld: Rood krijgt 1 + 2 + 2 + 3 + 1 = 9 punten voor zijn abt:
Voorbeeld: Rood krijgt 1 + 2 + 2 + 3 + 1 = 9 punten voor zijn abt:- 1 punt voor de kloostertegel
- 2 punten voor de verticale kolom boven de kloostertegel (waarvan 1 van een driehoekige tegel)
- 2 punten voor de verticale kolom onder de kloostertegel (waarvan 1 van een driehoekige tegel)
- 3 punten voor de horizontale rij links van de kloostertegel (waarvan 2 van driehoekige tegels)
- 1 punt voor de horizontale rij rechts van de kloostertegel die uit één enkele driehoekige tegel bestaat
>> Burchten in Duitsland – Afbouwen van Duitse burchten
- Er is, buiten de algemene overwegingen hierboven, geen officiële verheldering beschikbaar hoe Duitse burchten werken in combinatie met de Halflingen.
- Opmerkingen:
- Huisregel: In navolging van de officiële uitspraak over kloosters kan een Duitse burcht als afgebouwd worden beschouwd als deze volledig omringd wordt door vierkante tegels of vakken waarop één of twee Halflingen liggen.
- Huisregel: Op grond van de officiële spelregels voor kloosters kun je voor een Duitse burcht 2 punten tellen voor de tegel met de Duitse burcht, plus 1 punt per omliggende tegel (ongeacht of dat een vierkante of driehoekige is).
>> Kleine gebouwen – Gebied waarop het Kleine gebouw effect heeft
- Buiten de algemene overwegingen hierboven zijn er geen officiële verhelderingen met betrekking tot het combineren van Kleine gebouwen met de Halflingen.
- Opmerking:
- Huisregel: Een klein gebouw heeft alleen effect op de Halfling-tegel waar deze op ligt, en heeft geen effect op de andere Halfling, mocht die er zijn, die hetzelfde vierkante vak deelt. Deze overweging volgt uit het feit dat een Halfling als één enkele tegel geldt en kleine gebouwen de een hele tegel raken. [12]
Gemeenschapsspelregels
>> Inleiding
Dit deel geeft een onofficiële set basis-gemeenschapsspelregels om valkuilen te vermijden als je met de Halflingen speelt. Het zijn geen officiële spelregels, maar ze helpen wel om een aantal kwesties op te lossen die het gevolg zijn van het gebrek aan spelregels voor de de uitbreiding zelf en voor de combinatie met andere uitbreidingen.
De basisspelregels van Carcassonne definiëren het gedrag en de werking op grond van een vierkant raster van tegels en gaten. Het probleem met de Halflingen vloeit voort uit het gebrek aan een complete set spelregels die alle mogelijke gevallen dekt dat een vierkant vak bezet wordt door een driehoekige tegel (en een driehoekig gat overlaat) of door twee driehoekige tegel.
Driehoekige tegels worden als aparte tegels gezien, wat gevolgen heeft voor verschillende basismechanismes van het spel. De driehoekige gaten zijn echter een serieuze bron van aanhoudende meningsverschillen. De onvolledige verhelderingen op de spelregels voor de Halflingen hebben een mijnenveld achtergelaten met slechts enkele aanwijzingen waar spelers alles uit proberen te wringen om de antwoorden te krijgen die nooit officieel door HiG bevestigd zullen worden.
Met dit in het achterhoofd en na in het vorige deel de spelregels, verhelderingen, openstaande vragen en een aantal huisregels voor het combineren van de Halflingen met andere uitbreidingen beschreven te hebben, zullen we nu proberen om enkele algemene opmerkingen te maken die als een korte gids kunnen dienen door voornoemd materiaal.
>> Redenen
Er zijn twee principes die als hoeksteen dienen:
- Driehoekige tegels zijn aparte tegels
- Driehoekige gaten gedragen zich, afhankelijk van de context, op twee verschillende manieren:
- Een driehoekig gat kan zich als een heel gat gedragen, bijvoorbeeld in een project
- Een driehoekig gat kan genegeerd worden, bijvoorbeeld bij het verplaatsen van een speelstuk
Onderstaande tabel geeft een overzicht van de verschillende situaties waarin er problemen kunnen ontstaan en doet daar een toepasselijke uitspraak over. Maar laten we eerst de spelsituaties waar we het over hebben benoemen:
- Doorlopen van het landschap: welke gevolgen hebben driehoekige tegels en gaten voor verschillende projecten, zoals een weide of een stad
- Projectplaatsing: welke gevolgen hebben driehoekige tegels en gaten voor het plaatsen van een project zoals een abdij
- Afgebouwd zijn van een project: welke gevolgen hebben driehoekige tegels en gaten voor het afgebouwd beschouwen van een project zoals een stad of een klooster
- Puntentelling van projecten: welke gevolgen hebben driehoekige tegels en gaten voor de puntentelling van een project zoals een Duits klooster
- Zetten of verplaatsen van speelstukken: welke gevolgen hebben driehoekige tegels en gaten voor mechanismes rondom speelstukken; bijvoorbeeld de draak
- Berekenen van bereik/baan: welke gevolgen hebben driehoekige tegels en gaten op het bereik van een toren of de baan van een vliegtuig
>> Hoe ga je om met de driehoekige tegels en gaten
Belangrijke herinnering: Driehoekige tegels worden als aparte tegels gezien. Houd dit in het achterhoofd bij het zetten van meeples, andere speelstukken of bij de puntentelling van projecten.
Onderstaande tabel geeft een overzicht van de gemeenschapsspelregels voor tegenstrijdige situaties.
| Gedrag bij driehoekige tegels en driehoekige gaten | ||||||
|---|---|---|---|---|---|---|
| Gat gedrag | Doorlopen landschap | Projectplaatsing | Afgebouwd zijn van project | Puntentelling project | Zetten / verplaatsen speelstuk | Bereik / baan berekenen |
| Een gat | Weide (1) | Weide | Brug | |||
| Stad, Weg | Stad, Weg | Stad, Weg | ||||
| Genegeerd | Abdij (2) | Klooster, Cultusplaats, Abdij, Tuin, Duits klooster (monnik) | Klooster, Cultusplaats, Abdij, Tuin, Duits klooster (monnik) | Draak | Toren, Vliegtuig (3) | |
| Duits klooster (abt) | ||||||
| Vlooienfiche | ||||||
- Opmerkingen:
- (1) - Doorlopen weide: Het zetten van een herenboerderij kan het doorlopen van weiden veranderen als die op een kruispunt wordt gezet waar oorspronkelijk gescheiden weiden elkaar raken waardoor die samengevoegd worden
- (2) - Abdij leggen: Om voor het leggen van een abdij in aanmerking te komen mogen er aan de vier zijden geen vierkante gaten zijn
- (3) - Vliegtuig: Als een vliegtuig dat een diagonale baan volgt op een vierkant vak landt waar twee driehoekige tegels naast elkaar liggen (m.a.w. beide hebben dezelfde vliegafstand), mag de speler zelf kiezen op welke tegel geland wordt
>> Hoe ga je om met de herenboerderij
Daarnaast zijn dit de gemeenschapsspelregels voor de herenboerderij:
- Spelregels voor het zetten: De herenboerderij wordt gezet op het kruispunt van vier rechte hoeken waarbij alle kwadranten geheel of gedeeltelijk bezet zijn en in het midden samenkomen. Dat wil zeggen dat de herenboerderij altijd op een stabiele ondergrond gezet moet worden. Op zo'n kruispunt kunnen 3 (met een dubbele) tot 8 (allemaal Halflingen) tegels samenkomen, en ze mogen daar uitsluitend weiden hebben om er een herenboerderij te mogen zetten.
- Doorlopen van het landschap: De herenboerderij voegt alle weiden die het kruispunt raken waar deze gezet is samen. De puntentelling voor weiden vindt dus op de gebruikelijke manier plaats. Elke aanvullende driehoekige tegel die in een gat dat onder de herenboerderij overgebleven is wordt gelegd, bestendigt de reeds aangenomen weideverbinding.
>> Hoe ga je om met bruggen
Een brug kan over twee Halflingen worden geplaatst die een vierkant veld innemen als beide uiteinden in een veld liggen. De brug zal ook moeten voldoen aan de andere gebruikelijke plaatsingsregels.
De volgende overwegingen zijn ook belangrijk, aangezien een brug over twee tegels wordt gezet:
- Zetten van een horige: Als er een horige op de brug wordt gezet, moet die duidelijk op één van beide helften worden gezet, dat wil zeggen aan één van beide Halflingen die eronder ligt worden toegewezen. Dit is bijvoorbeeld noodzakelijk als er met de draak of de pest wordt gespeeld om te weten wanneer een horige op de brug geraakt wordt.
- Puntentelling: De brug telt voor 1 wegdeel per onderliggende Halfling, dat wil zeggen, twee tegels in dit geval. [13]
>> Hoe ga je om met Kleine Gebouwen
Kleine gebouwen die op een Halfling-tegel worden gelegd hebben alleen effect op die driehoekige tegels. Als hetzelfde vierkante vak gedeeld wordt met een andere Halfling-tegel, wordt die niet geraakt.
Tegelverdeling
Halflingen I (Spielbox)
Halflingen II (Cundco)
Voetnoten
Kijk op de Pictogrammen pagina voor uitleg over en licensering van de pictogrammen.
- ↑
 Wordt er met minder dan 6 spelers gespeeld, dan krijgt elke speler toch maar 2 tegels. (3/2015)
Wordt er met minder dan 6 spelers gespeeld, dan krijgt elke speler toch maar 2 tegels. (3/2015)
- ↑
 Als alternatief kun je, als er minder dan 6 spelers zijn, ervoor kiezen om iedere speler net zolang tegels te laten trekken of kiezen tot de tegels op zijn en elke speler evenveel tegels heeft (bijv. bij 4 spelers krijgen ze er elk 3). (3/2015)
Als alternatief kun je, als er minder dan 6 spelers zijn, ervoor kiezen om iedere speler net zolang tegels te laten trekken of kiezen tot de tegels op zijn en elke speler evenveel tegels heeft (bijv. bij 4 spelers krijgen ze er elk 3). (3/2015)
- ↑
 Als er met zowel Halflingen I en II wordt gespeeld, is er geen consensus over het aantal tegels per persoon. Technisch gezien zijn het twee verschillende mini-uitbreidingen, dus zouden spelers er 2 uit elke set kunnen nemen. Anderzijds, omdat ze dezelfde spelregels hebben functioneel als één grotere uitbreiding gezien kunnen worden, kunnen de spelers ook in totaal twee Halflingen nemen. (3/2015)
Als er met zowel Halflingen I en II wordt gespeeld, is er geen consensus over het aantal tegels per persoon. Technisch gezien zijn het twee verschillende mini-uitbreidingen, dus zouden spelers er 2 uit elke set kunnen nemen. Anderzijds, omdat ze dezelfde spelregels hebben functioneel als één grotere uitbreiding gezien kunnen worden, kunnen de spelers ook in totaal twee Halflingen nemen. (3/2015)
- ↑
 Het schaap op de tegel telt elke keer dat een herder op een ermee verbonden weide zijn schapen naar de stal drijft als een “permanent” schaapfiche. (11/2014)
Het schaap op de tegel telt elke keer dat een herder op een ermee verbonden weide zijn schapen naar de stal drijft als een “permanent” schaapfiche. (11/2014)
- ↑
 De cirkelvormige graancirkel op de Halfling-tegel is een joker. Dat betekent dat de speler die deze tegel aanlegt zelf mag besluiten of hij die als schild, mestvork of knuppel wordt ingezet. (11/2014)
De cirkelvormige graancirkel op de Halfling-tegel is een joker. Dat betekent dat de speler die deze tegel aanlegt zelf mag besluiten of hij die als schild, mestvork of knuppel wordt ingezet. (11/2014)
- ↑
 Onderstaande voorbeelden tonen de gevolgen van de slecht-gedefinieerde spelregels aangezien er gevallen zijn dat er geen officiële uitspraak is over wanneer een stad is afgebouwd.
Onderstaande voorbeelden tonen de gevolgen van de slecht-gedefinieerde spelregels aangezien er gevallen zijn dat er geen officiële uitspraak is over wanneer een stad is afgebouwd.
 Voorbeeld 2: De aanwezigheid van een driehoekig gat in een stad veroorzaakt een conflict in de spelregels:
Voorbeeld 2: De aanwezigheid van een driehoekig gat in een stad veroorzaakt een conflict in de spelregels:- Volgens de spelregels van het basisspel is deze stad niet afgebouwd omdat er geen gat in zit;
- Aan de andere kant wordt een gat van een halve tegel in de spelregels van “Halflingen” niet als een echt gat gezien, en dus zou de stad als afgebouwd moeten worden beschouwd.
Vergelijkbare gevallen kunnen zich kunnen zich voordoen als besloten moet worden of een weg is afgebouwd als die onderbroken wordt door een driehoekig gat.
- ↑
 Driehoekige gaten in weiden zijn ook een open vraag: het is onduidelijk die het landschap onderbreken en derhalve weiden kunnen scheiden.
Driehoekige gaten in weiden zijn ook een open vraag: het is onduidelijk die het landschap onderbreken en derhalve weiden kunnen scheiden.
- ↑
 De puntentelling van een afgebouwde stad of weg verloopt volgens de gebruikelijke regels en een driehoekige tegel telt mee als normale tegel.
De puntentelling van een afgebouwde stad of weg verloopt volgens de gebruikelijke regels en een driehoekige tegel telt mee als normale tegel.
- ↑
 Op grond van de spelregel dat Halfling-tegels ook meetellen net als vierkante tegels, zijn kloosters afgebouwd als het vak met het klooster evenals de acht omringende vakken door tenminste één tegel belegd zijn, ongeacht of dat een vierkante of een Halfling-tegel is. De aanwezigheid van driehoekige gaten in deze vakken doet niet ter zake.
Op grond van de spelregel dat Halfling-tegels ook meetellen net als vierkante tegels, zijn kloosters afgebouwd als het vak met het klooster evenals de acht omringende vakken door tenminste één tegel belegd zijn, ongeacht of dat een vierkante of een Halfling-tegel is. De aanwezigheid van driehoekige gaten in deze vakken doet niet ter zake.
- ↑
 Onderstaande afbeelding toont de puntentelling van een afgebouwd klooster met omliggende Halflingtegels.
Onderstaande afbeelding toont de puntentelling van een afgebouwd klooster met omliggende Halflingtegels.
- ↑
 Het doorlopen van het landschap heeft gevolgen voor de telling van weiden. Er zijn gevallen die niet door de spelregels of latere verhelderingen gedekt worden.
Het doorlopen van het landschap heeft gevolgen voor de telling van weiden. Er zijn gevallen die niet door de spelregels of latere verhelderingen gedekt worden.
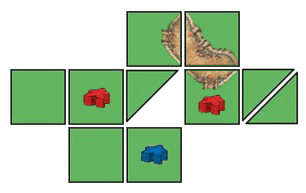 Voorbeeld: Het onbepaald of rood en blauw op dezelfde weide liggen, aangezien het onduidelijk is of het driehoekige gat in de afbeelding de weide wel of niet onderbreekt. De spelers zullen daarover zelf tot een uitspraak moeten komen en het resultaat is volkomen anders bij het tellen van de stad in dit voorbeeld:
Voorbeeld: Het onbepaald of rood en blauw op dezelfde weide liggen, aangezien het onduidelijk is of het driehoekige gat in de afbeelding de weide wel of niet onderbreekt. De spelers zullen daarover zelf tot een uitspraak moeten komen en het resultaat is volkomen anders bij het tellen van de stad in dit voorbeeld:- Geval 1 - De weiden zijn verbonden: In dat geval heeft rood de meerderheid op de weide en krijgt 3 punten voor de stad. Blauw krijgt 0 punten.
- Geval 2 - De weiden zijn niet verbonden: In dit geval delen rood en blauw de weide links en krijgen daar ieder 3 punten voor. Bovendien ligt alleen rood ook nog in de weide rechts en krijgt daar 3 punten voor.
- ↑
 Met de oude spelregels zou een klein gebouw dat op een Halfling-tegel ligt beide driehoekige tegels die hetzelfde vierkante vak delen geraakt hebben aangezien ze voor de puntentelling als één tegel worden gezien.
Met de oude spelregels zou een klein gebouw dat op een Halfling-tegel ligt beide driehoekige tegels die hetzelfde vierkante vak delen geraakt hebben aangezien ze voor de puntentelling als één tegel worden gezien.
- ↑
 Dit is noodzakelijk uit oogpunt van consistentie. Als de weg die met de brug verbonden is met een lus onder de brug doorloopt, telt de weg onder de brug mee voor twee tegels en dus hoort het deel wat over de brug loopt hetzelfde aantal tegels moeten tellen. In een notendop, het aantal tegels waar de brug voor staat moet overeenkomen met het aantal tegels haar hij op staat aangezien elke tegel apart geteld wordt bij het tellen van een weg.
Dit is noodzakelijk uit oogpunt van consistentie. Als de weg die met de brug verbonden is met een lus onder de brug doorloopt, telt de weg onder de brug mee voor twee tegels en dus hoort het deel wat over de brug loopt hetzelfde aantal tegels moeten tellen. In een notendop, het aantal tegels waar de brug voor staat moet overeenkomen met het aantal tegels haar hij op staat aangezien elke tegel apart geteld wordt bij het tellen van een weg.